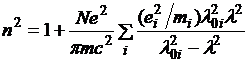, (3.2.7)

где N - плотность частиц (число частиц в единице объема), m и е – масса и заряд электрона соответственно, - резонансные длины волн, - вынуждающие осцилляции электрические силы. В широком спектральном диапазоне, включающем обычный ультрафиолет, видимую область и ближнюю инфракрасную область, кварцевое стекло прозрачно и данная формула Солмейера применима с очень высокой точностью [5, 7].

Явление, возникновение которого связано с характерными частотами, на которых среда поглощает электромагнитное излучение вследствие осцилляции связанных электронов, и которое определяет уширение длительности светового импульса после его прохождения через дисперсионную среду, называется в технике волоконно-оптической связи материальной дисперсией [5]:

(3.2.8)

где коэффициент М(λ) называется удельной материальной дисперсией. На длине волны λ = 1276 нм у кварца величина , следовательно коэффициент материальной дисперсии M(λ) = 0 (см. рис. 3.2). При длине волны λ > 1276 нм M(λ) меняет знак и принимает отрицательные значения, в результате чего на длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация М(λ) и N(λ). Длина волны, при которой это происходит, называется дли­ной волны нулевой дисперсии . Обычно указывается некоторый диапазон длин волн, в пре­делах которых может варьироваться для данного конкретного оптического волокна.

Результирующая дисперсия складывается из волноводной и материальной и называется хроматической дисперсией. Дисперсию в оптических волокнах принято характеризовать коэффициентом дисперсии или удельной дисперсией, измеряемом в пс/(нм·км). Коэффициент дисперсии численно равен увеличению длительности светового импульса (в пикосекундах), спектральная ширина которого равна 1 нм, после прохождения отрезка ОВ длиной 1 км. Значение коэффициента хроматической дисперсии определяется как D(λ) = М(λ) + N(λ). Удельная дисперсия имеет размерность пс/(нм·км).

При допущениях, которые исходят из результатов опытов для различных веществ, из выражения (3.2.7) может быть получена приближенная формула зависимости показателя преломления от длины волны:

(3.2.9)