ГРП – среда с малой степенью ионизации: в газе нейтральных атомов или молекул в небольшом количестве присутствуют ионы и электроны. Потенциальная энергия кулоновского взаимодействия частиц пренебрежимо мала по сравнению с кинетической: е/4peоd << kT, где d – радиус Дебая–Гюккеля, определяющий линейных масштаб действия кулоновских сил:

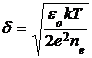. (1)

Здесь eо – электрическая постоянная, nе – концентрация электронов.

В ГРП преобладают столкновения с нейтральными частицами. Тепловое движение заряженных частиц мало, чем отличается от движения нейтральных частиц, если отсутствуют внешние электромагнитные поля, – применимы соотношения молекулярно-кинетической теории [1]. В термодинамически равновесном ГРП концентрация частиц также как и в газовой плазме определяется формулой Саха (1920 г.). Для ГРП удобно представить результат относительно концентрации электронов:

ne = (2me)3/4(kT)1/4Ро1/2h3/2exp(-ejи/(kT)), (2)

где Ро – давление нейтрального газа, eφи=W1 -W2 – энергия ионизации. В смеси газов φи относится к легкоионизируемым компонентам, даже если их количество nли мало.

В классической газовой плазме локальное нарушение квазинейтральности приводит к возникновению плазменных затухающих колебаний с частотой

wn = 2π νn:

, (3) где me – масса электрона.

Плазменные колебания могут развиваться и существовать на интервале времени между двумя столкновениями tо = 1/νо. Если же wntо< 1, то этот коллективный процесс развиваться не будет. Неравенство характеризует переход от плазмы к ГРП [1]. Сравним определительные соотношения для ГРП и плазмы: 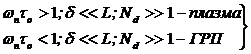. (4)

Здесь L – характерный линейный масштаб исследуемой среды, Nd – количество заряженных частиц в сфере Дебая. Различие между газовой плазмой и ИГ определяется соотношением для частот. Хотя понятие плазменной частоты для ИГ не имеет физической реальности. Невыполнение в (4) вторых соотношений (плазменных приближений) приводит к нарушению условия квазинейтральности, а невыполнение третьих, – приводит к нарушению электрической однородности: газ становится слабоионизованным, тепловое движение “маскирует” кулоновские взаимодействия: kT>e2(4πεoδ)–1.

В ГРП время флуктационного разделения зарядов tn = 1/wn необходимо заменить на время релаксации локального заряда, – максвелловским временем tМ. Время tМ определяется через равенство токов смещения и токов проводимости:

. (5)

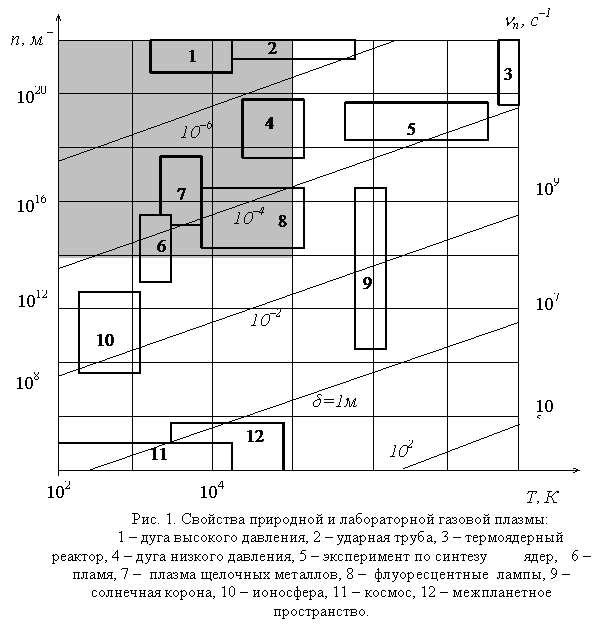
Для исследуемой среды tМ имеет значение на много порядков большее по сравнению с подобной величиной для металлических проводников. Для ИГ при изменении ne от 1015 до 1018 м–3 и значение tМ изменяется от мс до мкс. На рис. 1 приводятся параметры различных видов ионизованного газа [2]. «Техническая» плазма размещается в закрашенной левой верхней четверти рисунка.

Колебательные и волновые процессы в исследуемой среде определяются по воздействию на электрическую компоненту. Выделяются три области частот:

ВЧ – n > 1/teо, СЧ – 1/teо ≤ n ≥ 1/tМ, НЧ – n < 1/tМ . (6)

Между wn, teо , tМ существует однозначная зависимость: wn2 teо tМ = 1. Если tm>te0, то tn>te0 и наоборот, если tm<teо, то tn<teо. Первая пара неравенств характеризует свойства ГРП, вторая – газовой плазмы. Следовательно, в качестве временнόго критерия подобия можно использовать безразмерную величину: Та = tМ/teо. (7)

Рассматриваемая в работе среда удовлетворяют условию: Та>>1 [1].