Рассмотрим электрет в ячейке, показанной на рис. 13. Плотность тока, протекающего во внешней цепи и в образце j(t), складывается из тока проводимости в диэлектрике j(х,t) и тока смещения в диэлектрике

которые

являются

функциями двух

переменных - координаты х и времени t

(61)

Данное утверждение вытекает из хорошо известного уравнения непрерывности для плотности тока:

из которого с учетом одномерности задачи и формулы Максвелла вытекает:

Интегрируя данное выражение по координате, получаем:

где f(t)- произвольная функция времени, выполняющая роль «постоянной» интегрирования. Она имеет размерность плотности

тока

и вследствие независимости от координаты может быть принята

за «полный» ток, протекающий в цепи –j(t).

Ток проводимости j(x,t) в общем случае состоит из двух компонент: тока равновесной (собственной, омической) проводимости

связанного с движением в электрическом поле собственных носителей заряда, и тока неравновесной проводимости

связанного с движением в поле электрета внедренных неравновесных носителей заряда; q - заряд неравновесного носителя, μ - подвижность неравновесного носителя, п(х,t) - концентрация неравновесных носителей заряда, зависящая от координаты х и времени t, λ проводимость диэлектрика.

j(x,t)=λE(x,t)+qμn(x,t)E(x,t). (62)

В нашей задаче мы пренебрегаем неравновесной проводимостью, поскольку носители прочно удерживаются ловушками и не способны двигаться в электрическом поле. Тогда в (62) ток проводимости будет состоять

из одной компоненты - тока собственной проводимости. Выражение (61) примет вид:

(63)

В воздушном зазоре будет протекать тот же полный ток j(t), но там он будет чистым током смещения, т.к. никаких носителей заряда нет, и не будет зависеть от координаты:

(64)

С другой стороны, на основании формулы (43) . Поверхностный потенциал при релаксации зависит от времени. Дифференцируя Е1

по времени и подставляя в формулу (64), приходим к выражению для полного тока:

(65)

Проинтегрируем (63) по координате от 0 до s:

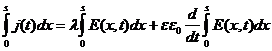
(предполагается, что λ не зависит от координат - однородный диэлектрик). Т.к. 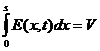, то

(66)

Из последней формулы видно, что если верхний электрод касается поверхности электрета или напылён на его поверхность, релаксация за счет собственной проводимости наблюдаться не будет: V = 0 и j(t) :=0. Поэтому наличие воздушного зазора является необходимым условием наблюдения релаксации за

счет собственной проводимости.

Формулы (65) и (66) дают возможность получить дифференциальное уравнение релаксации поверхностного потенциала, связанной с омической проводимостью. Заменяя в (66) плотность тока по формуле (65), после небольших преобразований приходим к уравнению:

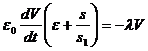(67)

В случае, когда электрет свободный (нет

верхнего электрода, s1→∞), либо при условии, что s1>>s:

или (68)

Решение полученного уравнения зависит от того, при каких условиях наблюдается релаксация потенциала - изотермических или при линейном возрастании температуры. Действительно, коэффициент электропроводности диэлектрика λ, при Т=сопst постоянен, а с ростом Т увеличивается. Например, если имеется кристаллический диэлектрик с шириной запрещенной зоны ΔЕ, то

.(69)

Рассмотрим случай изотермической релаксации Коэффициент перед dt в уравнении (68) не зависит от времени, тогда общее решение уравнения будет иметь вид;