Внутри волновода длина волны отличается от длины волны, в свободном пространстве и наблюдается большая дисперсия, т. е. зависимость скорости распространения волн от частоты и различие между фазовой и групповой скоростью.

Прямоугольный волновод.

Рассмотрим простейшую структуру поля в прямоугольном, волноводе при распространении в нем электромагнитного поля. Она называется основным типом волны прямоугольного волно­вода и обозначается ТЕ01. Электрическое поле имеется только в направлении у. Это удовлетворяет граничному условию Et =0 на стенках параллельно плоскости xz, образующих верх и низ волновода. На боковых стенках Еу тоже равно нулю. Поэтому для простейшего распределения поля в прямоугольном волноводе, которое удовлетворяет граничным условиям, зависимость Еу от z должна быть синусоидальной, т.е.

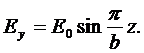(8)

Величина π/b в этом уравнении вводится для того, чтобы Еу рав­нялось нулю на боковых стенках волновода, т. е. при z=0 и z=b. Этот же результат дает и реше­ние уравнения поля.

Составляющая Еу, оставаясь перпендикулярной плоскости xz, распространяется в направлении оси х, и поэтому ее зависимость от z и х будет следующая:

так как

Таким образом, простейшая волна ТЕ01 характеризуется тем, что вдоль большой стороны b поперечного сечения волновода укладывается один максимум поля, а вдоль меньшей стороны сечения а поле не изменяется.

Составляющая магнитного поля Hz также должна меняться синусоидально по z, для того чтобы нормальная составляющая магнитного поля на боковых ее стенках волновода обращалась в ноль, как этого требуют граничные условия. Вдоль оси рас­пространения волны х составляющая Нz изменяется как cos (wt-βgx). Магнитные силовые линии должны быть замкну­ты, поэтому выходят из поперечной плоскости и идут вдоль волновода в направлении оси х, образуя продольную состав­ляющую магнитного поля Нх. Эта составляющая должна меняться, как , так как она максимальна на боковых стенках волновода, где магнитные силовые линии изгибаются и идут вдоль волновода. Кроме того, она должна быть сдвинута на π/2 по отношению к Еу и Нz в их пространственном измене­нии вдоль оси х. Так как электрическое поле направлено толь­ко по оси у, составляющие Ех и Еz равны нулю. Что касается компоненты Ну, то она равна нулю для этой волны в силу гра­ничных условий. Таким образом, уравнения, описывающие пол­ное поле волны ТЕ01 будут:

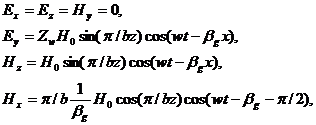(9)

где b — ширина волновода, λg - длина волны в волноводе, βg = 2π/ λg — фазовая постоянная, Hо — амплитуда магнитного-поля, создаваемая источником в центре волновода в плоскости х = 0, Zw — волновое сопротивление волновода [6].

Волновое сопротивление Zw есть отношение напряженности электрического поля к напряженности магнитного в плоскости, перпендикулярной к направлению распространения волны.

Длина волны в волноводе.

Каждая составляющая электрического поля должна удовле­творять волновому уравнению. Составляющая Еу, таким обра­зом, должна удовлетворять уравнению

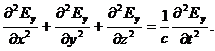(10)

Для волны TE01Ey определяется из уравнения (9). Подстав­ляя Еу в уравнение (10), получим

(11)

где =2π/λg а c - скорость света в свободном пространстве. Так как

(12)

где λ - длина волны генератора в свободном пространстве, то из уравнения (11) получим