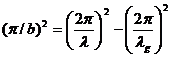(13)

Это равенство дает

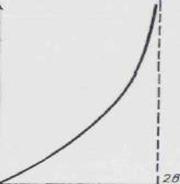
(14)

Отсюда видно, что длина волны в трубе больше, чем в свобод­ном пространстве. Это вызвано тем, что фазовая скорость рас­пространения волн в волноводе боль­ше, чем скорость распространения в свободном пространстве. Дифференцируя (11), получим выражение для группо­вой скорости

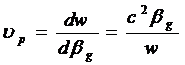(15)

фазовая скорость будет

(16)

Кривая зависимости λg от λ, соответст­вующая уравнению (14), показана на рис. 2. С приближением λ к 2b λg не­ограниченно нарастает. Если λ>2b, то из уравнения (2.30) следует, что дли­на волны в волноводе становится мнимой величиной. Это означает, что при λ>2b всякое распространение волны в волноводе прекращается. Поэтому за предельную длину волны в прямоугольном волноводе с волной TE01 берут λпр = 2b. Ра­венство

(17)

справедливо для любого типа волны, любого волновода любого сечения при условии, что значение λg соответствует тому типу волны и тому поперечному сечению, которые в этом случае рас­сматриваются.

Для того чтобы понять особенности распространения элек­тромагнитной волны в прямоугольном волноводе и наличие в нем критической волны, необходимо исходить из того, что поле в нем есть результат сложения двух плоских волн. В самом деле, рассмотрим плоскости равных фаз и направление распро­странения двух одинаковых плоских электромагнитных волн, изображенных на рис.3. Пусть направления распространения

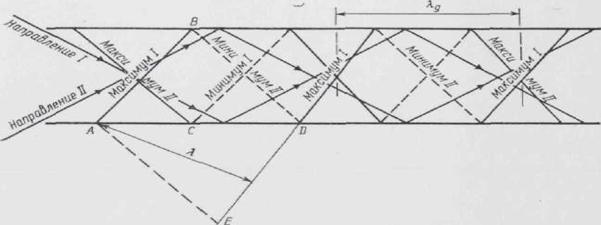
Рис. 3. Плоскости равных фаз в прямоугольном волноводе

волн I и II образуют одинаковые углы падения с боковыми стенками волновода. Сплошными линиями, перпендикулярными к направлениям волн I и II, показаны плоские фронты этих волн с фазой, соответствующей максимуму бегущей синусои­дальной волны для некоторого момента времени. Пунктирные линии соответствуют плоскостям минимумов бегущей волны. Как это видно из построения, на стенках в местах пересечения максимумов одной волны с минимумом другой автоматически выполняются граничные условия. Фронты максимумов плоских волн пересекаются посередине волновода под такими же угла­ми, как и фронты минимумов. При увеличении длины плоской волны X вертикальные углы между фронтами максимумов и ми­нимумов также увеличиваются и, таким образом, возрастают углы падения и отражения. Это и обусловливает появление пре­дельной волны. Действительно, рассмотрим луч, соответствую­щий направлению волны I и ее фронт, где находится в данный момент максимум бегущей волны. Угол падения луча обозначим через θ. Из треугольника EOF (рис. 4) следует

λ/2=bcosθ, λ=2bcosθ

Следовательно, максимальная длина волны, которая может распространяться по волноводу, λпр =2b. В этом случае угол 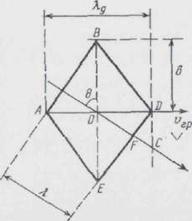падения и отражения θ = 0 и фронт плоской волны параллелен оси волно­вода. При таком падении волна будет отражаться от стенки к стенке в вер­тикальном направлении и вдоль вол­новода распространяться не будет. От­сюда следует, что длина волны в вол­новоде, измеряемая вдоль оси волно­вода λg, больше длины волны в сво­бодном пространстве λ, и так как λпр =2b, то cosθ= λ/λпр С другой сто­роны,