2. Выберем "движущуюся" систему таким образом, чтобы в начальный момент точка, изображающая ее начало координат, т.е. совпадала с точкой, изображающей начало координат "неподвижной" системы, т.е. , а скорость движения системы была бы направлена только по

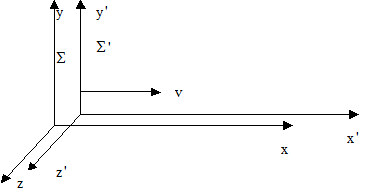Если мы также учтем требование изотропности пространства, то линейные преобразования для системы отсчета , выбранной указанным образом, запишутся в виде Здесь отсутствуют члены, содержащие и в выражениях и , в силу изотропности пространства и наличия единственного выделенного направления вдоль оси , соответственно постановке задачи. На этом же основании в выражениях для и отсутствуют члены, пропорциональные, соответственно, и , а коэффициенты при и одинаковы. Члены, содержащие и , отсутствуют в выражениях для и в силу того, что ось все время совпадает с осью . Последнее было бы невозможно, если бы и зависели от и .

3. Изотропность предполагает также симметричность пространства. В силу же симметрии ничто не должно измениться в формулах преобразования, если изменить знаки и , т.е. одновременно изменить направление оси и направление движения системы . Следовательно, (d) Сравнивая эти уравнения с предыдущими () получаем: