. Вместо удобно ввести другую функцию , так, чтобы выражалось через ипосредством соотношения Согласно этому соотношению, - симметричная функция. Используя это соотношение, преобразования (d) можно записать в виде 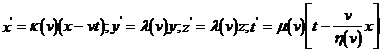(e), причем все входящие в эти формулы коэффициенты суть симметрии функции .

4. В силу принципа относительности

обе системы, "движущаяся" и "неподвижная", абсолютно эквивалентны, и поэтому обратные преобразования от системы кдолжны быть тождественно прямым от к. Обратные преобразования должны отличаться лишь знаком скорости , т.к. системадвижется относительно системывправо со скоростью , а система движется относительно системы (если последнюю считать неподвижной), влево со скоростью . Следовательно, обратные преобразования должны иметь вид 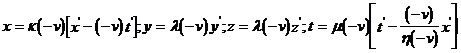. (f) Сравнивая эти преобразования с (e), получаем . Но в силу симметрии получаем, что , т.е. . Очевидно, имеет смысл лишь знак (+), т.к. знак (-) давал бы при перевернутую по и систему. Следовательно . Замечая, что коэффициенты - тоже симметричные функции , первое и последнее уравнение из (e) и (f) можно записать в виде: А) , а) , В) , в) . Умножая А) на , В) на и складывая, получим . 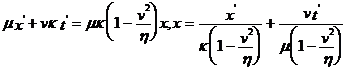Сравнивая это выражение с а), получаем . Откуда имеем